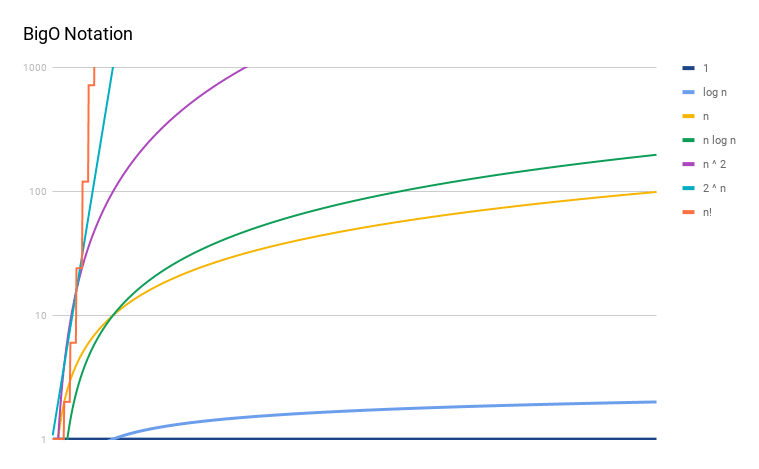Big O คืออะไร ?

ปกติแล้วเวลาที่เราเขียนโค้ด เราจะใช้เวลากับการหาข้อมูล ศึกษาความรู้ใหม่ๆ หรือนั่งแก้บัคให้โปรแกรมของเราทำงานได้ พอเขียนเสร็จแล้วก็ลองรันทดสอบ ถ้าทำงานได้อย่างที่ต้องการไม่มีบัคใดๆ ก็เป็นอันเสร็จสิ้น เอาไปส่ง หรือเอาไปใช้งานได้  ซึ่งกว่าจะเสร็จจนรันได้ก็น่าจะเหนื่อยและใช้เวลาไปมากแล้ว

แต่ว่าโปรแกรมของเรามันทำงานได้ดีแค่ไหนล่ะ ? ถ้าโปรแกรมของเรา BigO เยอะ แล้วเคสที่เราทำการทดสอบมันก็ไม่ได้ใช้เวลามากพอ เราก็อาจจะไม่ทันสังเกตุเห็นถึงขนาดของ BigO ในโปรแกรมของเรา พอนำไปใช้งานจริงแล้วเจอข้อมูลที่ต้องนำมาประมวลผลหลากหลายขึ้น อาจจะทำให้โปรแกรมของเราทำงานช้ากว่าที่คิดเอาไว้ หรือถึงขั้นใช้งานไม่ได้เลยทีเดียว

แล้ว Big(O) คืออะไร ?

ถ้าโปรแกรมที่เราเขียนมี array ที่มีข้อมูลผู้ใช้จำนวน 100 ข้อมูล แล้วเราต้องการใช้ข้อมูลของผู้ใช้คนหนึ่ง ก็ต้องไล่ข้อมูลตั้งแต่ตัวแรกเพื่อหาข้อมูลที่เราต้องการ ถ้าโชคดีหน่อยก็จะเจอตั้งแต่ตัวแรกๆ แต่ถ้าโชคร้ายก็จะเจอที่ตัวสุดท้ายเลย ซึ่งถ้าเกิดกรณีนี้ขึ้นมาหมายความว่าโปรแกรมของเราจะต้องใช้เวลาและทรัพยากรเท่ากับการทำงาน 100 รอบ แล้วถ้าโปรแกรมของเราใหญ่ขึ้นมีข้อมูลมากขึ้น ข้อมูลของเราจะไม่มีแค่จำนวน 100 แน่ๆ อาจจะเป็นหลักล้าน หรือ หลัก 100ล้าน ก็จะต้องรันตามจำนวนข้อมูลเหล่านั้น จำนวนการทำงานในกรณีที่มากที่สุดนี้แหละที่เราเรียกว่า BigO ซึ่งจะบ่งบอกถึงว่าโปรแกรมของเราสามารถกินทรัพยากรได้หนักแค่ไหน การเขียนโปรแกรมให้มี BigO น้อยที่สุดจึงเป็นสิ่งที่ควรใส่ใจเป็นอย่างยิ่ง

Big O มีกี่ชนิด ?

เวลาพูดถึง Big O Notation เราจะเรียกกันว่า O(n) ซึ่ง n จะใช้แทนจำนวนหรือขนาดของข้อมูลที่จะถูกนำไปประมวลผลด้วยอัลกอริทึมของเรา ถ้าลองดูในวิกิพีเดียเรื่อง Big O Notation จะเห็นว่ามีอยู่เป็นสิบชนิด แต่ในบทความนี้เราจะยกมาแค่ 7 ชนิด ที่น่าจะเข้าใจได้ง่ายและเพียงพอต่อการคำนวน BigO ในโค้ดของเรา โดยเราจะโฟกัสที่จำนวนรอบหรือเวลาที่ใช้ในการทำงานของแต่ละชนิด

1. O(1) : constant

สำหรับ BigO ตัวแรกนี้เป็น BigO ที่ดีที่สุด ไม่ว่า input จะเป็นอะไรก็ใช้เวลาทำงานเพียง 1 ครั้งเท่าเดิมเสมอ เช่น การเช็คว่าตัวเลข input เป็นเลขคู่หรือเลขคี่ จากโค้ดตัวอย่างด้านล่างนี้ ไม่ว่าใส่ค่า 0 หรือ 9999999 ก็ทำงานด้วยการ mod ด้วย 2 ครั้งเดียวเท่ากัน

def evenOrOdd(num):
   if (num % 2 == 0):
       print("even")
   else:
       print("odd")
 
evenOrOdd(0)
evenOrOdd(9999999)

2. O(log n) : logarithmic

เป็น BigO ที่ดีเยี่ยม โดยเป็นการทำงานที่จะลดจำนวนลูปลงครึ่งนึงทุกครั้งที่ทำเสร็จไป 1 รอบ ตัวอย่างอัลกอรึทึมที่มีเป็นชนิดนี้ก็คือการทำ Binary Search ที่จะค้นหาตำแหน่งของตัวเลขที่เราต้องการใน array ที่เรียงลำดับเอาไว้แล้ว

เช่นเรามี array อยู่หนึ่งตัวที่ตัวเลขข้างในเรียงจากน้อยไปมาก และต้องการหา ตำแหน่งของเลขที่ต้องการ ถ้าค้นหาตำแหน่งด้วยวิธี Binary Search ก็จะลดจำนวนรอบที่จะต้องวนลูปเพื่อค้นหาลงทุกครั้งที่ยังไม่เจอ

def binarySearch(arr, value, first, last):
   if last >= first:
       mid = first + (last - first) // 2
       if arr[mid] == value:
           return mid
       elif arr[mid] > value:
           return binarySearch(arr, value, first, mid - 1)
       else:
           return binarySearch(arr, value, mid + 1, last)
   else:
       return -1
 
 
numArray = [1, 2, 7, 10, 22, 31]
number = 22
 
result = binarySearch(numArray, number, 0, len(numArray) - 1)
print(result)

3. O(n) : linear

BigO ชนิดนี้ยังถือว่าทำงานได้ดีอยู่ โดยจะใช้เวลาในการทำงานเท่ากับ input ตัวอย่างที่เห็นภาพง่ายที่สุดคือการค้นหาตำแหน่งของข้อมูลที่ต้องการจากใน array ที่ไม่ได้เรียงข้อมูล ซึ่ง BigO จะนับจากเคสที่เลวร้ายที่สุด เช่นการที่ข้อมูลที่เราต้องการอยู่ตำแหน่งสุดท้ายใน array เหมือนโค้ดต่อไปนี้

def searchNumber(arr, value):
 for i in range(len(arr)):
   if(arr[i] == value):
     return i
 
numArray = [7, 16, 2, 0, 5, 1, 30]
number = 30
 
result = searchNumber(numArray, number)
print(result)

4. O(n log n) : linearithmic

สำหรับชนิดนี้ถือว่ามีความเร็วระดับกลางๆ คือเป็นการทำงานลูปแบบ n รอบ ที่มีลูปแบบ log n รอบอยู่ข้างใน ตัวอย่างอัลกอริทึมที่เข้าเคสนี้ก็คือการ Merge Sort ซึ่งการทำงานยาวนิดหน่อย ลองตามไปอ่านอย่างละเอียดใน วิกิพีเดีย หรือลองดูใน เว็บนี้ ได้

5. O(n^2) : quadratic

BigO ชนิดใช้เวลาในการทำงานเลยระดับที่เรียกว่ากลางๆ จนเริ่มเข้าขั้นแย่แล้ว เพราะว่าเวลาในในการทำงานจะเพิ่มขึ้น 4 เท่า เมื่อข้อมูลเพิ่มขึ้น 2 เท่า การใช้งานที่มี BigO ระดับ เช่น การค้นหาข้อมูลที่ซ้ำกันใน array

def duplicateCheck(arr):
 for i in range(len(arr)):
   a = arr[i]
   for j in range(i+1, len(arr)):
     b = arr[j]
     print(a, b)
     if(a == b):
       return "duplicated"
 return "not duplicate"
 
numArray = [1,3,5,9]
 
result = duplicateCheck(numArray)
print(result)

6. O(2^n) : exponential

BigO ขั้นนี้เข้าขั้นวิกฤตแล้ว ข้อมูลเพียงแค่นิดเดียวก็มีการทำงานที่มหาศาล

def fibonacci(n):
    if n==1:
        return 0
    elif n==2:
        return 1
    else:
        return (fibonacci(n-1)+fibonacci(n-2))  
print(fibonacci(5))
print(fibonacci(21))

7. O(n!) : factorial

ชนิดสุดท้ายที่ยกมาในวันนี้เรียกได้ว่าเลวร้ายที่สุดสำหรับ BigO อัลกอริทึมที่ใช้ในชีวิตจริงก็ตามชื่อของ BigO นี้เลยก็คือการคำนวนค่า factorial

def factorial(num):
 if(num == 1):
   return 1
 for i in range(0, num):
   return num * factorial(num-1)
 
print(factorial(9))

แถมกราฟสรุปเวลาในการประมวลผลของ BigO แต่ละชนิด โดยขนาดข้อมูลเพิ่มขึ้นในแกน x และเวลาเพิ่มขึ้นในแกน y จะเห็นว่า BigO ชนิดหลังๆใช้เวลาเพิ่มขึ้นมากกกกกกกก ดูจากกราฟแล้วก็น่าจะพอเข้าใจถึงความสำคัญของการคิด BigO ในโปรแกรมของเราว่าสำคัญขนาดไหน เพราะถ้าไม่ระวังให้ดี โปรแกรมอาจจะทำงานนานเป็นชาติ หรือถึงขนาดที่ทำงานไม่ได้เลยทีเดียว